Le Perron borné/Numéro 16 - OCTOBRE 2011 : Différence entre versions
| Ligne 5 : | Ligne 5 : | ||
| − | + | ==Divers== | |
Version du 1 novembre 2011 à 17:10

|
|

|
xxxxxxxxxx
Divers
Problèmes Impossibles
L' histoire des «Problèmes Impossibles ?»
C'est sous ce titre que fut publié pour la première fois dans une revue scientifique le premier casse-tête. En effet, on peut penser que ces problèmes sont insolubles tant les hypothèses semblent insuffisantes, et pourtant la solution est unique !
Les énoncés de cette rubrique sont inspirés par la même idée: poser des questions auxquelles la réponse semble impossible devant la pauvreté des hypothèses. Pourtant, elles se résolvent toutes, avec de la logique, mais aussi une haute idée de l'aptitude à raisonner des personnages de ces histoires.
Et voici trois petits problèmes pour cogiter pendant vos weekend; Certains de ces problèmes sont extraits des questions du championnat international de jeux mathématiques et logiques.
Problème n° 9 – La roue de la vie
Dans un monastère trente moines se livrent quotidiennement à un bien curieux cérémonial.
A chaque repas c'est à dire trois fois par jour, et cela cinquante-deux semaines par an, sept jours sur sept (il y a donc un ou deux jours de repos chaque année), les moines se réunissent et s'assoient, régulièrement répartis autour d'une très grande table circulaire.
Ils portent tous un numéro de 1 à 30 sur le devant de leur robe de bure. Le Père Inférieur, le numéro 1, préside et se place toujours sur la même chaise et à la même place. Les autres moines se répartissent à leur gré, à condition d'obéir à la Règle suivante :
La somme des numéros de deux voisins quelconques doit toujours être égale à la somme des numéros portés par les deux moines qui leur sont diamétralement opposés. De plus, à chaque fois, la disposition globale des trente moines doit être nouvelle (celles-ci sont notées soigneusement depuis de longues années).
Mais un jour un des moines s'inquiète du nombre de dispositions possibles. Le Père Inférieur lui explique pourtant : "Notre tradition représente la roue de la vie, mon frère, nous respectons cette règle depuis la fondation du monastère il y a 1400 ans et bien d'autres après nous la continuerons ! Une légende dit que, lorsqu'on ne trouvera plus de nouvelle disposition, la vie cessera sur terre !".
Combien de temps durera encore cette cérémonie ?
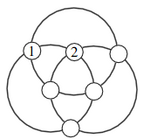
Problème n° 10 – Les six disques
(Extrait de la finale internationale des jeux mathématiques - Mai 2006)
On a posé six jetons numérotés de 1 à 6 sur les grands cercles.
La somme des numéros des jetons posés sur un même grand cercle est toujours la même.
Retrouvez la place des numéros 3 à 6.
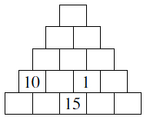
Problème n° 11 – La pyramide des différences
(Extrait de la finale internationale des jeux mathématiques - Mai 2006)
Dans les cases de cette pyramide, on a inscrit les nombres de 1 à 15 en respectant la règle suivante :
chaque nombre situé dans une case posée sur deux autres cases, est égal à la différence entre les nombres écrits dans ces deux autres cases (le plus grand moins le plus petit).
Retrouvez la place des nombres effacés.
Solution des problèmes précédents :
Problème n° 6 – Les 25 mathématiciens :
Vous avez reconnu Thalès, Pythagore, Euclide, Al-Kashi, Gauss, ...... Cliquez ici pour la solution détaillée...
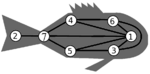
Problème n° 7 – Arrangement des nombres - Le poisson :
Ce problème n'admet deux solutions. Une représentée ci-contre, l'autre étant la symétrie Cliquez ici pour la solution détaillée...
Problème n° 8 – Le repas des moines :
Le nombre de moines malades est 8. Cliquez ici pour la solution détaillée...
Agenda
Vous voulez partager des infos, des documents, des liens internet, des ouvrages avec nos
confrères ou réagir à un article, n’ hésitez pas à me contacter sur la page de discussion de la revue ou
à l’adresse suivante : LePerronBorne at ARGELg.be