Le Perron borné/Numéro 17 - AVRIL 2012 : Différence entre versions
(→Divers) |
|||
| Ligne 5 : | Ligne 5 : | ||
==Divers== | ==Divers== | ||
| − | + | eedssssd | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Problèmes Impossibles== | ==Problèmes Impossibles== | ||
Version du 21 mars 2012 à 13:09

|
|

|
....
Divers
eedssssd
Problèmes Impossibles
L' histoire des «Problèmes Impossibles ?»
C'est sous ce titre que fut publié pour la première fois dans une revue scientifique le premier casse-tête. En effet, on peut penser que ces problèmes sont insolubles tant les hypothèses semblent insuffisantes, et pourtant la solution est unique !
Les énoncés de cette rubrique sont inspirés de la même idée: poser des questions auxquelles la réponse semble impossible devant la pauvreté des hypothèses. Pourtant, elles se résolvent toutes, avec de la logique, mais aussi une haute idée de l'aptitude à raisonner des personnages de ces histoires.
Et voici trois petits problèmes pour cogiter pendant vos weekend.
Certains de ces problèmes sont extraits des questions du championnat international de jeux mathématiques et logiques.
Si trouvez la solution à l'un de ces problèmes, merci de nous la faire parvenir en la publiant sur la la page de discussion de ce Perron Borné.
Problème n° 12 – Le dé sur l'échiquier
Un dé classique se trouve au départ sur la case en bas à gauche d’un échiquier.
Une arête du dé a la même longueur qu’un côté d’une case. A chaque mouvement, le dé tourne autour d’une arête vers une case adjacente, mais seulement vers la droite ou vers le haut (jamais vers la gauche ou vers le bas).
Pour un observateur fixe, sans compter la case de départ, combien le dé peut-il atteindre de cases de l’échiquier en se trouvant orienté exactement comme sur la case de départ ?
(Extrait de la finale national des jeux mathématiques - 2006)
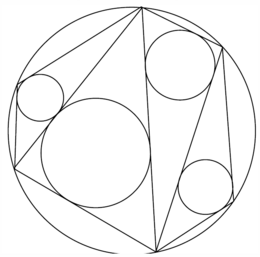
Problème n° 13 – Le partage de San Gaku
San Gaku a partagé sa propriété entre ses quatre enfants. C’est un hexagone dont la somme des longueurs de deux côtés consécutifs est toujours égale à 149 mètres.
La part de chaque enfant est un terrain triangulaire dont une piscine circulaire tangente chaque côté. Les sommets de l’hexagone sont situés sur une route circulaire dont le rayon est égal à la somme des rayons des piscines.
Quelle est la plus grande longueur d’un côté de l’hexagone arrondie au mètre le plus proche ? (Extrait de la finale internationale des jeux mathématiques - Mai 2006)
Problème n° 14 – Les trois graces
Nous retrouvons notre groupe de géomètres qui se réunissent toujours en fin de journée dans le bar de Madame Hypatie.
La patronne, comme d’habitude leur pose une colle en nous demandant de déterminer à quel étage l’immeuble, qui compte cinq étages, habitent les trois jeunes filles Adèles, Béatrice et Caroline.
Elle nous apprend :
- que les trois beautés habitent des étages différentes
- que Béatrice habite plus bas que caroline
- qu'Adèles n'habite pas entre Béatrice et Caroline.
Voyant que cela ne nous suffit pas, elle déclare qu'elle va communiquer à Francis l'étage habité par Béatrice ainsi que celui habité par Caroline.
Elle tend un morceau de papier à Francis.
"Et Adèle ?", demande Francis.
Posant son doit sur sa bouche, Madame Hypatie déclare qu'elle va communiquer à Jean-Yves l'étage habité par Adèle ainsi que celui fréquenté par Béatrice.
"Et Caroline ?", demande Jean-Yves après consultation du papier correspondant.
Se tournant vers moi, Madame Hypatie me tend alors une feuille où elle à écrit à quel étage vivent respectivement Adèle et Béatrice.
"Et Caroline ?", lui demandais-je.
Elle présente alors à Patrice un morceau de papier sur lequel elle a inscrit l'étage de Caroline.
"Saurez-vous retrouver l'étage des deux autres ? "demanda-t-elle.
Patrice dut également avouer son ignorance.
Et vous, pouvez vous déterminer à quel étage habite les trois filles ?
Solution des problèmes précédents :
Problème n° 9 – La roue de la vie :
Vous avez bien sure trouvé 319.333.000 années... Cliquez ici pour la solution détaillée...
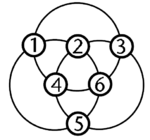
Problème n° 10 – Arrangement des nombres - Les 6 disques :
Ce problème admet deux solutions dont une est représentée ci-dessous Cliquez ici pour la solution détaillée...
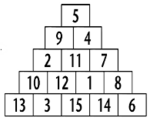
Problème n° 11 – La pyramide des différences :
Ce problème n'admet qu'une solution représentée ci-dessous Cliquez ici pour la solution détaillée...
Vous voulez partager des infos, des documents, des liens internet, des ouvrages avec nos
confrères ou réagir à un article, n’ hésitez pas à me contacter sur la page de discussion de la revue ou
à l’adresse suivante : LePerronBorne at ARGELg.be