Le Perron borné/Numéro 24 - DECEMBRE 2013 : Différence entre versions
| Ligne 3 : | Ligne 3 : | ||
===11111=== | ===11111=== | ||
| − | [[Image: | + | [[Image:image.jpg|left|500px]] |
| − | [ | + | [URL lien] |
| − | |||
Version du 11 août 2013 à 18:03

|
|

|
111
11111
[URL lien]
Rappel : photos des évènements organisés par l'ARGELg
Les photos des évènements publiques suivants sont disponibles sur myPictureTown
- Les photos de la remise du Brevet Royal
- Les photos de l'urban tour 2012 et Chaudfontaine 2012, deux activités externes auxquels plusieurs de nos membres ont représenté notre Association.
Problèmes Impossibles
L' histoire des «Problèmes Impossibles ?»
C'est sous ce titre que fut publié pour la première fois dans une revue scientifique le premier casse-tête. En effet, on peut penser que ces problèmes sont insolubles tant les hypothèses semblent insuffisantes, et pourtant la solution est unique !
Les énoncés de cette rubrique sont inspirés de la même idée: poser des questions auxquelles la réponse semble impossible devant la pauvreté des hypothèses. Pourtant, elles se résolvent toutes, avec de la logique, mais aussi une haute idée de l'aptitude à raisonner des personnages de ces histoires.
Et voici quelques petits problèmes posés précédemment et non résolus (inutile de chercher la solution sur le wiki) pour cogiter pendant vos vacances, que ce soit à la plage, à la montagne, dans l'avion, ou même chez vous.
Certains de ces problèmes sont extraits des questions du championnat international de jeux mathématiques et logiques.
Si vous trouvez la solution à l'un de ces problèmes, merci de nous la faire parvenir en la publiant sur la la page de discussion de ce Perron Borné.
Solution des problèmes précédents :
Problème n° 20 – Les trois pions
La solution est atteinte en 28 mouvements
Problème n° 21 – Les deux rectangles
Ce problème admet une seule solution qui est 4566242 mm2
Problème n° 22 – Pliage
Ce problème admet une seule solution qui est de 115,2 mm.
Problème n° 23 – Un hendécagone
Ce problème admet une seule solution: 1 solution : 7 carrés et 13 triangles comme indiqué ci-contre
Nouveaux problèmes:
Problème n° 24 – Le parallélogramme
Philippe va acquérir une nouvelle propriété en forme de parallélogramme. Lorsqu’on lui demande quelle en est la superficie, il répond simplement : « Mon terrain a un côté qui mesure exactement 100 mètres. Chaque diagonale mesure un nombre entier de mètres. La somme des longueurs des diagonales vaut exactement 500 mètres. De plus, l’aire du terrain est un nombre entier de mètres carrés ». Quelle est la contenance de cette parcelle de terrain?
(Extrait de la finale national des jeux mathématiques - 2011 - coefficient 16)
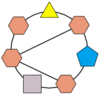
Problème n° 25 – Les Polygones Autoréférents
Placez tous les chiffres de 1 à 7, à raison d'un par polygone, de façon que :
- dans le triangle, le chiffre soit égal au premier chiffre (à gauche) du produit des deux chiffres auxquels il est relié ;
- dans le carré, le chiffre soit égal au dernier chiffre (à droite) du produit des deux chiffres auxquels il est relié ;
- dans le pentagone, le chiffre soit égal au premier chiffre (à gauche) de la somme des deux chiffres auxquels il est relié ;
- dans chaque hexagone, le chiffre soit égal au dernier chiffre (à droite) de la somme des deux, trois ou quatre chiffres auxquels il est relié.
(Extrait du quart-finale national des jeux mathématiques - 2012 - coefficient 14)
Problème n° 26 – Une boule dans un tétraèdre
Dans un carré de côté 2012 mm, on a tracé le patron de tétraèdre représenté ci-contre, où le sommet situé en haut à droite est relié aux milieux de deux côtés. On veut réaliser le tétraèdre et y enfermer une boule qui soit parfaitement tangente aux quatre faces du tétraèdre. Quel sera le diamètre de cette boule ?
(Extrait du quart-finale national des jeux mathématiques - 2012 - coefficient 18)
Agenda
Activités de l'ARGELg
- Le 19 septembre 2013 à 19h30 : La rénovation des ouvrages hydrauliques par la fibre de carbone, par ir. C. QUILINA, professeur invité à la HEPL ISIL.
- Le 24 septembre 2013 : GeoExpo, Le salon bisannuel des géomètres-experts.
- Le 14 (ou le 8) novembre et le 21 novembre 2013 à 17h30 : 2 ateliers de la pathologie animés par notre confrère monsieur F. WARGNIES.
Références
Vous voulez partager des infos, des documents, des liens internet, des ouvrages avec nos
confrères ou réagir à un article, n’ hésitez pas à me contacter sur la page de discussion de la revue ou
à l’adresse suivante : LePerronBorne at ARGELg.be