Le Perron borné/Numéro 16 - OCTOBRE 2011

|
|

|
xxxxxxxxxx
Divers
Raccourcir des vidéos YouTube pour une présentation
Quand vous faites une présentation, une vidéo YouTube peut offrir un morceau d'infotainment amusant. Ou peut-être voulez-vous envoyer des vidéos intéressantes par e-mail à des collègues ou les partager avec votre réseau social. Or ces vidéos sont souvent plus longues que vous ne le voudriez. Heureusement, il existe des façons simples de les réduire sur mesure.
Si vous n'avez besoin que d'un fragment d'une vidéo YouTube, vous avez plusieurs possibilités. Vous pouvez vous arranger pour que la vidéo ne commence pas au début : en ajoutant '#t=2m21s' à l'URL, la vidéo débutera à 2 minutes et 21 secondes. Une autre possibilité consiste à faire commencer et finir la vidéo à un moment déterminé. Vous pouvez découper un fragment d'une vidéo YouTube en ligne avec TubeChop en adaptant le temps de début et de fin. Recherchez d'abord la vidéo que vous voulez raccourcir. Copiez l'URL pour l'envoyer sur TubeChop. La vidéo commence à tourner avec des 'sliders' au bas de l'image. Avec ces sliders, vous pouvez régler le nouveau temps de début et de fin. Cliquez sur 'Chopit'. La vidéo raccourcie reçoit un URL et un code uniques que vous pouvez mettre dans vos slides, mails ou profils de réseau. Ainsi, vous ne fatiguerez pas votre public avec des informations inutiles mais pourrez vous concentrer sur le message essentiel.
Source : Martijn Aslander e.a., '175 lifehackingtips', Van Duuren Management, 2011
Problèmes Impossibles
L' histoire des «Problèmes Impossibles ?»
C'est sous ce titre que fut publié pour la première fois dans une revue scientifique le premier casse-tête. En effet, on peut penser que ces problèmes sont insolubles tant les hypothèses semblent insuffisantes, et pourtant la solution est unique !
Les énoncés de cette rubrique sont inspirés par la même idée: poser des questions auxquelles la réponse semble impossible devant la pauvreté des hypothèses. Pourtant, elles se résolvent toutes, avec de la logique, mais aussi une haute idée de l'aptitude à raisonner des personnages de ces histoires.
Et voici trois petits problèmes pour cogiter pendant vos weekend; Certains de ces problèmes sont extraits des questions du championnat international de jeux mathématiques et logiques.
Problème n° 9 – La roue de la vie
Dans un monastère trente moines se livrent quotidiennement à un bien curieux cérémonial.
A chaque repas c'est à dire trois fois par jour, et cela cinquante-deux semaines par an, sept jours sur sept (il y a donc un ou deux jours de repos chaque année), les moines se réunissent et s'assoient, régulièrement répartis autour d'une très grande table circulaire.
Ils portent tous un numéro de 1 à 30 sur le devant de leur robe de bure. Le Père Inférieur, le numéro 1, préside et se place toujours sur la même chaise et à la même place. Les autres moines se répartissent à leur gré, à condition d'obéir à la Règle suivante :
La somme des numéros de deux voisins quelconques doit toujours être égale à la somme des numéros portés par les deux moines qui leur sont diamétralement opposés. De plus, à chaque fois, la disposition globale des trente moines doit être nouvelle (celles-ci sont notées soigneusement depuis de longues années).
Mais un jour un des moines s'inquiète du nombre de dispositions possibles. Le Père Inférieur lui explique pourtant : "Notre tradition représente la roue de la vie, mon frère, nous respectons cette règle depuis la fondation du monastère il y a 1400 ans et bien d'autres après nous la continuerons ! Une légende dit que, lorsqu'on ne trouvera plus de nouvelle disposition, la vie cessera sur terre !".
Combien de temps durera encore cette cérémonie ?
Problème n° 10 – Les six disques
(Extrait de la finale internationale des jeux mathématiques - Mai 2006)
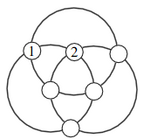
On a posé six jetons numérotés de 1 à 6 sur les grands cercles.
La somme des numéros des jetons posés sur un même grand cercle est toujours la même.
Retrouvez la place des numéros 3 à 6.
Problème n° 11 – La pyramide des différences
(Extrait de la finale internationale des jeux mathématiques - Mai 2006)
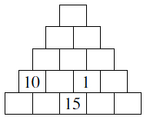
Dans les cases de cette pyramide, on a inscrit les nombres de 1 à 15 en respectant la règle suivante :
chaque nombre situé dans une case posée sur deux autres cases, est égal à la différence entre les nombres écrits dans ces deux autres cases (le plus grand moins le plus petit).
Retrouvez la place des nombres effacés.
Solution des problèmes précédents :
Problème n° 6 – Les 25 mathématiciens :
Vous avez reconnu Thalès, Pythagore, Euclide, Al-Kashi, Gauss, ...... Cliquez ici pour la solution détaillée...
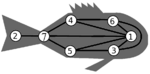
Problème n° 7 – Arrangement des nombres - Le poisson :
Ce problème n'admet deux solutions. Une représentée ci-contre, l'autre étant la symétrie Cliquez ici pour la solution détaillée...
Problème n° 8 – Le repas des moines :
Le nombre de moines malades est 8. Cliquez ici pour la solution détaillée...
Agenda
Vous voulez partager des infos, des documents, des liens internet, des ouvrages avec nos
confrères ou réagir à un article, n’ hésitez pas à me contacter sur la page de discussion de la revue ou
à l’adresse suivante : LePerronBorne at ARGELg.be