Problèmes Impossibles/Le pentagone

|
|

|
Enoncé
Béatrice vient d'hériter d'une parcelle de terrain en forme de pentagone non régulier. elle n'a pas encore vu le terrain, mais elle connaît déjà les éléments suivants :
- le pentagone est constitué de 2 petits côtés mesurant tous les deux 20 mètres de long, et de 3 grands côtés, eux aussi de même longueur,
- les deux petits côtés sont consécutifs et forment un angle droit à l'intérieur du terrain,
- le grand côté, non adjacent à un petit côté, est parallèle à un des deux petits côtés,
- aucun angle entre deux grands côtés n'est obtus.
Quelle est l'aire minimum de ce terrain ?
Solution
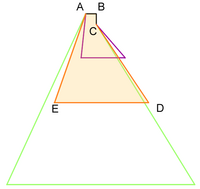
Nous avons donc deux côtés A-B et B-C de 20 m formant un angle droit en B ainsi que trois côtés identiques CD, DE et AE supérieur a 20 m avec ED parallèle à AB. La superficie du pentagone irrégulier ABCDE varie en fonction de la position des points D et E.
On peut facilement constater sur la figure ci-contre, que l'angle E augmente lorsque la superficie diminue (tracés vert, rouge et violet). L'angle E ne pouvant être obtus, la superficie minimum est obtenue lorsque E est droit.
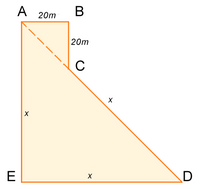
Dans cette situation, les triangles AED et ABC sont semblables, et les points A, C et D sont alors alignés.
Par simple application du théorème de Pythagore et en posant x la longueur d'un grand coté, nous obtenons :
<asciimath>(20*sqrt2+x)^2</asciimath> = <asciimath>2*x^2</asciimath>
ce qui donne <asciimath>x = (20*sqrt2)/( sqrt2 - 1)</asciimath> = 68,284 m
La superficie minimum de la parcelle est alors donnée par la somme des superficie des triangles ADE et ABC, c'est à dire <asciimath>1/2*[((20*sqrt2)/(sqrt2 - 1))^2+20^2]</asciimath> = 2531,37 m2