Redaction:Le perron Borné

|
|

|
Walonmap: nouvelles données disponibles[modifier]
Depuis janvier 2018, différentes données ont été ajoutées ou actualisées sur le Géoportail Walonmap :
- RAVeL
- Périmètres de reconnaissance économique (PRE)
- Schémas de Développement Communaux (SDC) au sens du CoDT
- Avant-projets et projets de modification du Plan de Secteur
- Biens classés et zones de protection
- CoDT - Schéma d'Orientation Local (SOL)
- Réseau routier régional et bornes kilométriques
- Projet Informatique de Cartographie Continue (PICC)
- Plans de mobilité & mobilité supra-communale
- Sites à réaménager de droit (SAR)
- Orthophotos 2017
- Zones de bruit
- Lignes du réseau TEC et arrêts
- Arbres et haies remarquables (AHREM)
- ...
==
???[modifier]
Problèmes Impossibles[modifier]
Problème n° 33 – Un hendécagone En juxtaposant des carrés tous identiques et des triangles équilatéraux de même côté que les carrés, François forme un polygone convexe à 11 côtés (un hendécagone) sans trou. Combien de carrés et combien de triangles équilatéraux François a-t-il utilisés si il a pris un minimum de pièces au total ? Note : trois sommets consécutifs de l'hendécagone ne peuvent pas être alignés.
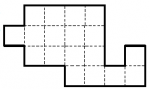
Problème n° 34 – Découpage
Découpez cette figure en deux parties identiques en suivant les lignes du quadrillage. Note : deux parties sont identiques si on peut les superposer, en retournant éventuellement l’une d’elles.
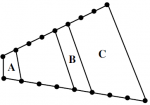
Problème n° 35 – Les quatre champs
Sur chacune des deux routes en ligne droite, des poteaux (points) sont régulièrement espacés. L'aire du champ A est prise pour unité. Celle du champ C est 2010 (la figure ne respecte pas les proportions). Quelle est l'aire du champ B
Solution des problèmes précédents[modifier]
Problème n° 30 – La fourmi dans le cube
Vous avez bien sûr trouvé une probabilité de 2/243
Problème n° 31 – Le parallélogramme
Les géomètres que vous êtres auront sans nul doute remarqués que c'est une simple application des formules de Héron et de Pythagore
le problème a deux solutions qui sont 16800 et 21000.
Problème n° 32 – Le jeu des verres
Les verres peuvent être remis à l'endroit en 4 coups minimum
Agenda[modifier]
Vous voulez partager des infos, des documents, des liens internet, des ouvrages avec nos
confrères ou réagir à un article, n’ hésitez pas à me contacter sur la page de discussion de la revue ou
à l’adresse suivante : LePerronBorne at ARGELg.be