Le Perron borné/Numéro 22 - MARS 2013 : Différence entre versions
(a déplacé Redaction:Le perron Borné vers Le Perron borné/Numéro 21 - NOVEMBRE 2012) |
m (Nouvelle version) |
||
| Ligne 1 : | Ligne 1 : | ||
| − | + | {{Perron Borné|21|DECEMBRE|2012}} | |
| + | |||
| + | |||
| + | ==Compte rendu du séminaire en Espagne== | ||
| + | |||
| + | par Gilles.marchal | ||
| + | |||
| + | |||
| + | ==L'ARGELg arbore un nouveau logo== | ||
| + | |||
| + | |||
| + | |||
| + | ==Rappel : photos des évènements organisés par l'ARGELg== | ||
| + | |||
| + | Les photos des évènements publiques suivants sont disponibles sur myPictureTown | ||
| + | |||
| + | * Les photos de [http://img.gg/yNN0Tpv la soirée de "Rentrée Académique 2011 - Titre Royal de l'AGELg"] | ||
| + | |||
| + | * Les photos de [http://img.gg/cNNoUYP la remise du Brevet Royal] | ||
| + | |||
| + | * Les photos de [http://img.gg/WNNo99O l'urban tour 2012] et [http://img.gg/nN9Z21e Chaudfontaine 2012], deux activités externes auxquels plusieurs de nos membres ont représenté notre Association. | ||
| + | |||
| + | ==Problèmes Impossibles== | ||
| + | [[Image:Perron15_Problème_Impossible.gif|right|200px]] | ||
| + | '''L' histoire des «Problèmes Impossibles ?»''' | ||
| + | |||
| + | C'est sous ce titre que fut publié pour la première fois dans une revue scientifique le premier casse-tête. En effet, on peut penser que ces problèmes sont insolubles tant les hypothèses semblent insuffisantes, et pourtant la solution est unique ! | ||
| + | |||
| + | Les énoncés de cette rubrique sont inspirés de la même idée: poser des questions auxquelles la réponse semble impossible devant la pauvreté des hypothèses. Pourtant, elles se résolvent toutes, avec de la logique, mais aussi une haute idée de l'aptitude à raisonner des personnages de ces histoires. | ||
| + | |||
| + | '''Et voici quelques petits problèmes posés précédemment et non résolus (inutile de chercher la solution sur le wiki) pour cogiter pendant vos vacances, que ce soit à la plage, à la montagne, dans l'avion, ou même chez vous.''' | ||
| + | |||
| + | Certains de ces problèmes sont extraits des questions du championnat international de jeux mathématiques et logiques. | ||
| + | |||
| + | '''Si vous trouvez la solution à l'un de ces problèmes, merci de nous la faire parvenir en la publiant sur la [[Discussion:Le_Perron_borné|la page de discussion]] de ce Perron Borné.''' | ||
| + | |||
| + | ====Solution des problèmes précédents :==== | ||
| + | '''Problème n° 12 – Le dé sur l'échiquier''' | ||
| + | <br />Le dé peut au maximum atteindre 15 cases | ||
| + | |||
| + | '''Problème n° 13 – Le partage de San Gaku''' | ||
| + | <br />Ce problème admet une seule solution qui est 111 métres | ||
| + | |||
| + | '''Problème n° 14 – Les trois graces''' | ||
| + | <br />Ce problème admet une seule solution: C'est le 5éme étage qui était indiqué sur la dernière feuille. | ||
| + | |||
| + | '''Problème n° 15 – Dames chinoises en solitaire''' | ||
| + | <br />Ce problème admet une seule solution: On peut au maximum placer 81 jeton sur le damier | ||
| + | |||
| + | '''Problème n° 17 – Les trimonos''' | ||
| + | <br />Le nombre maximum de cases vide est de 15. | ||
| + | |||
| + | '''Problème n° 18 – Les quatre Champs''' | ||
| + | <br />Ce problème admet une seule solution qui est 447 | ||
| + | |||
| + | '''Problème n° 19 – Le jardin de Yannick''' | ||
| + | <br />Ce problème admet une seule solution qui est 77 mètres (triangle de côtés 16, 28 et 33) | ||
| + | |||
| + | ====Nouveaux problèmes:==== | ||
| + | [[Image:Problemes_Impossibles_20_E01.png|right|120px|Les trois pions]] | ||
| + | '''Problème n° 20 – Les trois pions''' | ||
| + | |||
| + | Dans ce jeu, chaque mouvement consiste à déplacer un pion d’une case vers une case voisine vide. Deux cases sont voisines si elles se touchent par un côté. | ||
| + | |||
| + | On veut amener le pion n° 1 dans la case a, le pion n° 2 dans la case b et le pion n°3 dans la case c. | ||
| + | |||
| + | Combien de mouvements seront nécessaires, au minimum ? | ||
| + | |||
| + | ''(Extrait de la finale national des jeux mathématiques - 2011)'' | ||
| + | |||
| + | [[Image:Problemes_Impossibles_21_E01.png|right|100px|Les deux rectangles]] | ||
| + | '''Problème n° 21 – Les deux rectangles''' | ||
| + | |||
| + | Patrice doit implanter un bâtiment sur une parcelle rectangulaire de 10.11 m sur 20.11 m de façon a en optimiser la superficie. | ||
| + | |||
| + | Il sait que chacun des sommets du bâtiment, également rectangulaire, est sur un des côtés de la parcelle, à raison d’un sommet par côté. | ||
| + | |||
| + | Quelle est la superficie maximum que peut avoir le bâtiment implanté par Patrice ? | ||
| + | |||
| + | [[Image:Problemes_Impossibles_22_E01.png|right|350px|Pliage]] | ||
| + | '''Problème n° 22 – Pliage''' | ||
| + | |||
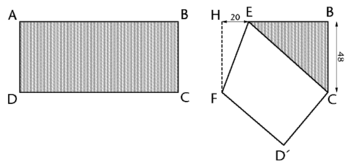
| + | On plie en deux une bande de papier rectangulaire ABCD selon EF de façon à amener A sur C (voir la figure). | ||
| + | En abaissant la perpendiculaire issue du point F sur la droite BE, on obtient le point H situé à 20 cm du point E (voir la figure). | ||
| + | |||
| + | Si le rectangle de papier a une largeur égale à 48 cm, quelle est sa longueur ? | ||
| + | |||
| + | ''(Extrait de la finale national des jeux mathématiques - 2011)'' | ||
| + | |||
| + | '''Problème n° 23 – Un hendécagone''' | ||
| + | |||
| + | En juxtaposant des carrés tous identiques et des triangles équilatéraux de même côté que les carrés, on forme un polygone convexe à 11 côtés (un hendécagone) sans trou. | ||
| + | |||
| + | Combien de carrés et combien de triangles équilatéraux a-t-on utilisés si elle a pris un minimum de pièces au total ? | ||
| + | |||
| + | Note : trois sommets consécutifs de l'hendécagone ne peuvent pas être alignés. | ||
| + | |||
| + | ''(Extrait de la finale national des jeux mathématiques - 2011)'' | ||
| + | |||
| + | ==Agenda== | ||
| + | |||
| + | *Le <font color="9A3334">'''27 Novembre 2012 à 18h30'''</font> Table ronde ayant pour sujet "Quelles sont les informations minimales qui doivent figurer sur les plans" (Marcel PONTHIER) | ||
| + | |||
| + | *A partir du <font color="9A3334">'''30 novembre 2012'''</font> les participants GeoFormation peuvent valider et télécharger leur attestations sur le site GeoFormation. | ||
| + | |||
| + | *Le <font color="9A3334">'''6 Décembre 2012 à 16h30'''</font> Assemblé Générale Obligatoire de l'ARGELg. | ||
| + | |||
| + | *A partir du <font color="9A3334">'''10 janvier 2013'''</font> les membres ARGELg peuvent télécharger leur attestations des tables rondes, Assemblées générales et Commission sur le site Argelg. | ||
| + | |||
| + | {{Perron_Borné_End|David Sibret|Jacques.houbart|Yanick.grignet|Gilles.marchal}} | ||
Version du 28 novembre 2012 à 15:10

|
|

|
Compte rendu du séminaire en Espagne
par Gilles.marchal
L'ARGELg arbore un nouveau logo
Rappel : photos des évènements organisés par l'ARGELg
Les photos des évènements publiques suivants sont disponibles sur myPictureTown
- Les photos de la remise du Brevet Royal
- Les photos de l'urban tour 2012 et Chaudfontaine 2012, deux activités externes auxquels plusieurs de nos membres ont représenté notre Association.
Problèmes Impossibles
L' histoire des «Problèmes Impossibles ?»
C'est sous ce titre que fut publié pour la première fois dans une revue scientifique le premier casse-tête. En effet, on peut penser que ces problèmes sont insolubles tant les hypothèses semblent insuffisantes, et pourtant la solution est unique !
Les énoncés de cette rubrique sont inspirés de la même idée: poser des questions auxquelles la réponse semble impossible devant la pauvreté des hypothèses. Pourtant, elles se résolvent toutes, avec de la logique, mais aussi une haute idée de l'aptitude à raisonner des personnages de ces histoires.
Et voici quelques petits problèmes posés précédemment et non résolus (inutile de chercher la solution sur le wiki) pour cogiter pendant vos vacances, que ce soit à la plage, à la montagne, dans l'avion, ou même chez vous.
Certains de ces problèmes sont extraits des questions du championnat international de jeux mathématiques et logiques.
Si vous trouvez la solution à l'un de ces problèmes, merci de nous la faire parvenir en la publiant sur la la page de discussion de ce Perron Borné.
Solution des problèmes précédents :
Problème n° 12 – Le dé sur l'échiquier
Le dé peut au maximum atteindre 15 cases
Problème n° 13 – Le partage de San Gaku
Ce problème admet une seule solution qui est 111 métres
Problème n° 14 – Les trois graces
Ce problème admet une seule solution: C'est le 5éme étage qui était indiqué sur la dernière feuille.
Problème n° 15 – Dames chinoises en solitaire
Ce problème admet une seule solution: On peut au maximum placer 81 jeton sur le damier
Problème n° 17 – Les trimonos
Le nombre maximum de cases vide est de 15.
Problème n° 18 – Les quatre Champs
Ce problème admet une seule solution qui est 447
Problème n° 19 – Le jardin de Yannick
Ce problème admet une seule solution qui est 77 mètres (triangle de côtés 16, 28 et 33)
Nouveaux problèmes:
Problème n° 20 – Les trois pions
Dans ce jeu, chaque mouvement consiste à déplacer un pion d’une case vers une case voisine vide. Deux cases sont voisines si elles se touchent par un côté.
On veut amener le pion n° 1 dans la case a, le pion n° 2 dans la case b et le pion n°3 dans la case c.
Combien de mouvements seront nécessaires, au minimum ?
(Extrait de la finale national des jeux mathématiques - 2011)
Problème n° 21 – Les deux rectangles
Patrice doit implanter un bâtiment sur une parcelle rectangulaire de 10.11 m sur 20.11 m de façon a en optimiser la superficie.
Il sait que chacun des sommets du bâtiment, également rectangulaire, est sur un des côtés de la parcelle, à raison d’un sommet par côté.
Quelle est la superficie maximum que peut avoir le bâtiment implanté par Patrice ?
Problème n° 22 – Pliage
On plie en deux une bande de papier rectangulaire ABCD selon EF de façon à amener A sur C (voir la figure). En abaissant la perpendiculaire issue du point F sur la droite BE, on obtient le point H situé à 20 cm du point E (voir la figure).
Si le rectangle de papier a une largeur égale à 48 cm, quelle est sa longueur ?
(Extrait de la finale national des jeux mathématiques - 2011)
Problème n° 23 – Un hendécagone
En juxtaposant des carrés tous identiques et des triangles équilatéraux de même côté que les carrés, on forme un polygone convexe à 11 côtés (un hendécagone) sans trou.
Combien de carrés et combien de triangles équilatéraux a-t-on utilisés si elle a pris un minimum de pièces au total ?
Note : trois sommets consécutifs de l'hendécagone ne peuvent pas être alignés.
(Extrait de la finale national des jeux mathématiques - 2011)
Agenda
- Le 27 Novembre 2012 à 18h30 Table ronde ayant pour sujet "Quelles sont les informations minimales qui doivent figurer sur les plans" (Marcel PONTHIER)
- A partir du 30 novembre 2012 les participants GeoFormation peuvent valider et télécharger leur attestations sur le site GeoFormation.
- Le 6 Décembre 2012 à 16h30 Assemblé Générale Obligatoire de l'ARGELg.
- A partir du 10 janvier 2013 les membres ARGELg peuvent télécharger leur attestations des tables rondes, Assemblées générales et Commission sur le site Argelg.
Vous voulez partager des infos, des documents, des liens internet, des ouvrages avec nos
confrères ou réagir à un article, n’ hésitez pas à me contacter sur la page de discussion de la revue ou
à l’adresse suivante : LePerronBorne at ARGELg.be